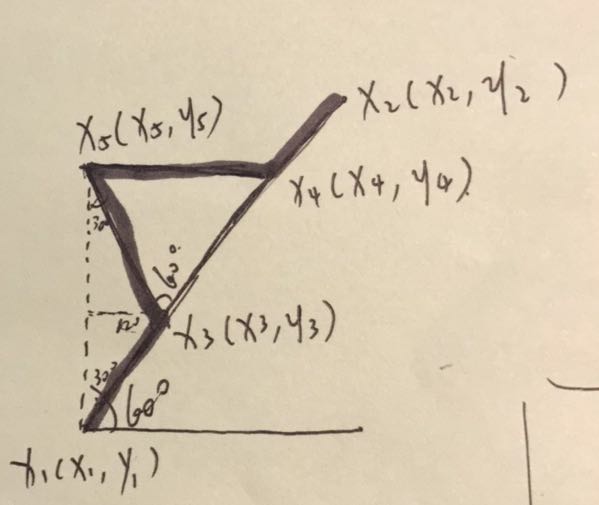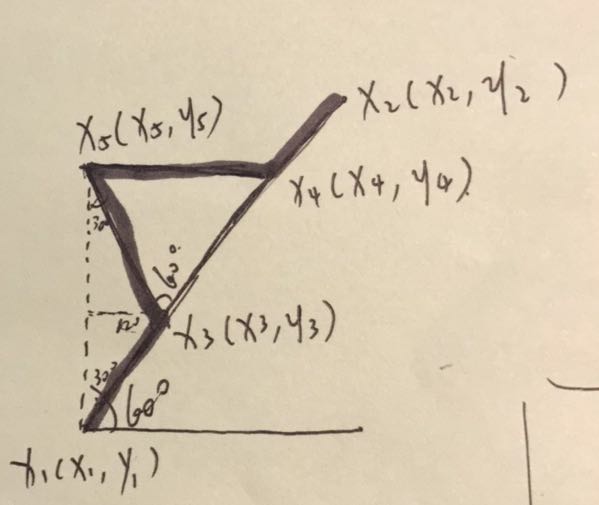1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
| <html lang="en">
<head>
<title>科赫雪花</title>
<meta charset="UTF-8">
<meta name="viewport" content="width=device-width, initial-scale=1">
</head>
<body>
<input type="range" id="range" max="5" min="1" step="1" value="1">
<canvas id="canvas" height="280" width="280"></canvas>
</body>
<script>
var canvas = document.getElementById("canvas");
function koch(ctx, x1, y1, x2, y2, n, m) {
ctx.clearRect(0,0,400,400);
var x3 = (x2 - x1) / 3 + x1;
var y3 = (y2 - y1) / 3 + y1;
var x4 = (x2 - x1) / 3 * 2 + x1;
var y4 = (y2 - y1) / 3 * 2 + y1;
var x5 = x3 + ((x2 - x1) - (y2 - y1) * Math.sqrt(3)) / 6;
var y5 = y3 + ((x2 - x1) * Math.sqrt(3) + (y2 - y1)) / 6;
n++;
if (n == m) {
ctx.moveTo(x1, y1);
ctx.lineTo(x3, y3);
ctx.lineTo(x5, y5);
ctx.lineTo(x4, y4);
ctx.lineTo(x2, y2);
ctx.stroke();
return false;
}
koch(ctx, x1, y1, x3, y3, n, m);
koch(ctx, x3, y3, x5, y5, n, m);
koch(ctx, x5, y5, x4, y4, n, m);
koch(ctx, x4, y4, x2, y2, n, m);
}
function draw(deep) {
var ctx = canvas.getContext("2d");
ctx.strikeStyle="#000";
ctx.beginPath();
var y=80+Math.cos(Math.PI/6)*200;
koch(ctx,150,y,250,80,0,deep);
koch(ctx,250,80,50,80,0,deep);
koch(ctx,50,80,150,y,0,deep);
}
draw(1);
var range=document.getElementById("range");
range.onchange=function(){
var r=~~range.value;
draw(r)
}
</script>
<style>
body {
text-align: center;
}
#canvas {
background-color: #fff;
}
</style>
</html>
|